Text compression

Program: Implement the tree-based Huffman coding for Unicode strings, implementing the tree structure yourself.

For this first part I implemented a binary tree to find the codes for each symbol.

1. The first thing that I did was to create a frequency table.
2. Then I put in pairs the lighter weights until the end of the list.
3. I searched the tree to find the codes for each leaf

I have done a web application to display the Huffman coding in a binary tree, this is the URL:

http://huffmandemo.appspot.com/

And here is the example:

After the decoding algorithm, I did take the text file that I wrote in binary, and I found the equivalent to the tree that I had already done.

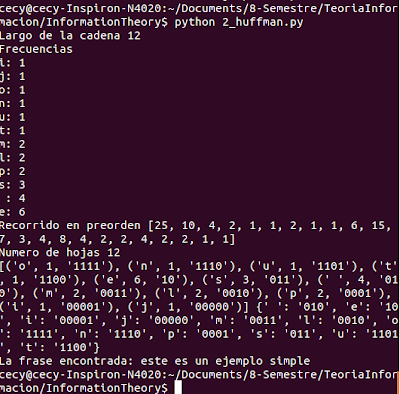
This is the example in the terminal encoding and decoding:

Analyze an experiment to determine the worst-case and typical-case complexity and compression ratio


I use texts of 3000 words, for the worst case I have done texts with the same frequency and for the typical case I take random Internet texts

Here I show some plots that I got when I did the experiment:

compression ratio

The best case is when all the probabilities of the symbols change in powers of 2. And the worst is when all the probabilities are equal.

The complexity of the algorithm is O(nlog n). Since it has an internal loop with logn complexity and then repeated n times, where n is the set of symbols.


And this is the code:


References

Huffman compression

Huffman coding