History
A5/1 is used in Europe and the U.S. A5/1 is a very weak encryption algorithm, developed in 1987, when GSM was not even considered for use in Europe. A5 / 2 is a safer alternative that was developed in 1989.
Security
There are some well-known attacks to the algorithm A5 / 1. In some attacks, expensive preprocessing stages are required, after the code is attacked in minutes or seconds. The weakness of the algorithm had been passive attacks using the assumption of known plaintext. In 2003 were identified serious weaknesses that could be exploited ciphertext attacks (active attack). Eli Biham and Nathan Keller demonstrated attacks against A5 / 1 and A5 / 3 that allow the attacker to decipher the conversation in real time from a GSM phone.
Attacks with knowledge of the plaintext
In 1997, Golic presented an attack based on solving sets of linear equations of computational complexity 2 ^ 4016.
Also in 2000, Eli Biham and Orr Dunkelman published an attack with a complexity of 2 ^ 3991. This attack requires 32 GB of data stored after a previous stage of computing 2 ^ 38.
Description
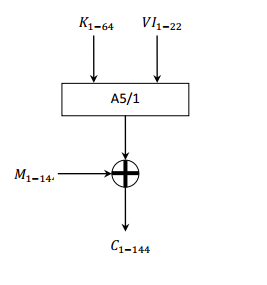
The transmission in GSM is performed in data blocks. Each block contains 114 bits available for information. A5 / 1 produces a 228-bit sequence of stream, which will serve as key encryption for message clear by Vernam algorithm (114 bits for a sense of call, and 114 for the other). It requires a user key of 64 bits (which is stored in the phone's SIM) together with an initialization vector 22 bits publicly known.
 |
| http://es.scribd.com/doc/25241410/46/Esquema-del-algoritmo-de-cifra-A5-1 |
 |
| http://en.wikipedia.org/wiki/A5/1 |
 |
| http://calliope.uwaterloo.ca/~ggong/ECE710T4/lec8-ch6b.pdf |
Initializing A5
1. The three shift registers are set to zeros. The output and function are most disabled.
2. The least significant bit of each row applies XOR each bit of the key for 64 cycles. At this point, the LFSR normally works.
3. The least significant bit of each row applies XOR each bit vector Initialization for 22 cycles. The LFSR is working normally.
4. The majority function F is enabled for 100 cycles and moving logs, the Movement is made taking the result of F.
5. Using the majority function, and enabling the output of each shift register bitsduring 228 cycles. The most significant bits of each register are operated by XOR output, the result of this operation results in a bit of the encryption key.
Majority function
- F (C1, C2, C3) = C1 C2 ⊕ C1 C3 ⊕ C2 C3 where C1, C2, C3 are the clock bits for records R1, R2, R3, respectively.
- If the bit clock of a record matches the function majority, that record moves. Otherwise, the register keeps its value.
- This function majority forces at least 2 of the moving records at any time.
- Clock sequence is irregular and depends on the key and Frame Number.
The clear message is operated by XOR with the first sequence of 144 bits (load data).
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| #!/usr/bin/python | |
| import random | |
| DEBUG = True | |
| ###las primeras tres funciones hacen lo mismo pero tienen diferente | |
| ###nombre para no confundir los pasos | |
| def mensaje(): | |
| '''Crea el mensaje que se va a cifrar | |
| ''' | |
| bits = 228 | |
| mensaje = [] | |
| for i in range(bits): | |
| mensaje.append(random.randint(0,1)) | |
| return mensaje | |
| def generaClave(): | |
| '''Genera una clave de usuario la que esta | |
| almacenada en la SIM de 64 bits | |
| ''' | |
| bits = 64 | |
| clave = [] | |
| for i in range(bits): | |
| clave.append(random.randint(0,1)) | |
| return clave | |
| def inicializacion(): | |
| '''Genera un vector de inicializacion publicamente | |
| conocido de 22 bits | |
| ''' | |
| bits = 22 | |
| v_init = [] | |
| for i in range(bits): | |
| v_init.append(random.randint(0,1)) | |
| return v_init | |
| def registros(): | |
| '''Se llenan en 0 los registros | |
| ''' | |
| R1 = [0 for i in range(19)] | |
| R2 = [0 for i in range(22)] | |
| R3 = [0 for i in range(23)] | |
| return R1, R2, R3 | |
| def aplica_xor(R1, R2, R3, clave): | |
| '''Se aplica xor a los registros | |
| ''' | |
| ###Posiciones clave del registro 1 | |
| r1_1= 18 | |
| r1_2= 17 | |
| r1_3= 16 | |
| r1_4= 13 | |
| ###Posiciones clave del registro 2 | |
| r2_1= 21 | |
| r2_2= 20 | |
| ###Posiciones clave del registro 3 | |
| r3_1= 22 | |
| r3_2= 21 | |
| r3_3= 20 | |
| r3_4= 7 | |
| for i in range(len(clave)): | |
| R1res = R1[r1_1] ^ R1[r1_2] | |
| R1res = R1res ^ R1[r1_3] | |
| R1res = R1res ^ R1[r1_4] | |
| R1.insert(0, clave[i] ^ R1res) | |
| R1.pop() | |
| R2res = R2[r2_1] ^ R2[r2_2] | |
| R2.insert(0, clave[i] ^ R2res) | |
| R2.pop() | |
| R3res = R3[r3_1] ^ R3[r3_2] | |
| R3res = R3res ^ R3[r3_3] | |
| R3res = R3res ^ R3[r3_4] | |
| R3.insert(0, clave[i] ^ R3res) | |
| R3.pop() | |
| return R1, R2, R3 | |
| def funcion_mayoria(R1, R2, R3, clave): | |
| ###Posiciones clave del registro 1 | |
| r1_1= 18 | |
| r1_2= 17 | |
| r1_3= 16 | |
| r1_4= 13 | |
| ###Posiciones clave del registro 2 | |
| r2_1= 21 | |
| r2_2= 20 | |
| ###Posiciones clave del registro 3 | |
| r3_1= 22 | |
| r3_2= 21 | |
| r3_3= 20 | |
| r3_4= 7 | |
| ###Bits de reloj | |
| c1 = 8 | |
| c2 = 10 | |
| c3 = 10 | |
| ###Numeros de ciclos | |
| ciclos = 100 | |
| uno = 0 | |
| dos = 0 | |
| for i in range(ciclos): | |
| #con esta formula obtenemos F(c1,c2,c3) que nos ayuda a determinar que | |
| #registro de desplazara | |
| numero = (R1[c1] and R2[c2])^(R1[c1] and R3[c3])^(R2[c2] and R3[c3]) | |
| if R1[c1] == numero: | |
| R1res = R1[r1_1] ^ R1[r1_2] | |
| R1res = R1res ^ R1[r1_3] | |
| R1res = R1res ^ R1[r1_4] | |
| R1.insert(0, R1res) | |
| R1.pop() | |
| if R2[c2] == numero: | |
| R2res = R2[r2_1] ^ R2[r2_2] | |
| R2.insert(0, R2res) | |
| R2.pop() | |
| if R3[c3] == numero: | |
| R3res = R3[r3_1] ^ R3[r3_2] | |
| R3res = R3res ^ R3[r3_3] | |
| R3res = R3res ^ R3[r3_4] | |
| R3.insert(0, R3res) | |
| R3.pop() | |
| return R1, R2, R3 | |
| def clave_cifrado(R1, R2, R3): | |
| ###Posiciones clave del registro 1 | |
| r1_1= 18 | |
| r1_2= 17 | |
| r1_3= 16 | |
| r1_4= 13 | |
| ###Posiciones clave del registro 2 | |
| r2_1= 21 | |
| r2_2= 20 | |
| ###Posiciones clave del registro 3 | |
| r3_1= 22 | |
| r3_2= 21 | |
| r3_3= 20 | |
| r3_4= 7 | |
| ciclos = 228 | |
| clave = [] | |
| for i in range(228): | |
| R1res = R1[r1_1] ^ R1[r1_2] | |
| R1res = R1res ^ R1[r1_3] | |
| R1res = R1res ^ R1[r1_4] | |
| R1.insert(0, R1res) | |
| k1 = R1.pop() | |
| R2res = R2[r2_1] ^ R2[r2_2] | |
| R2.insert(0, R2res) | |
| k2 = R2.pop() | |
| R3res = R3[r3_1] ^ R3[r3_2] | |
| R3res = R3res ^ R3[r3_3] | |
| R3res = R3res ^ R3[r3_4] | |
| R3.insert(0, R3res) | |
| k3 = R3.pop() | |
| clave.append(k1 ^ k2 ^ k3) | |
| return R1, R2, R3, clave | |
| def cifrar(mensaje, llave): | |
| cifrado = [] | |
| for i in range(len(mensaje)): | |
| cifrado.append(mensaje[i]^llave[i]) | |
| return cifrado | |
| def main(): | |
| #Inicializacion de A5 | |
| #Paso 1: los tres registros de desplazamiento se | |
| #ajustan en ceros. La salida y la funcion mayoria estan | |
| #deshabilitados | |
| mensaje_original = mensaje() | |
| clave = generaClave() | |
| v_init = inicializacion() | |
| R1, R2, R3 = registros() | |
| #Paso 2: al bit menos significativo de cada registro se aplica X0R | |
| #con cada bit de la clave durante 64 ciclos | |
| R1, R2, R3 = aplica_xor(R1, R2, R3, clave) | |
| #Paso 3: al bit menos significativo de cada registro se aplica XOR | |
| #con cada bit del vector de inicializacion durante 22 ciclos | |
| R1, R2, R3 = aplica_xor(R1, R2, R3, v_init) | |
| #Paso 4: La funcion mayoria F se habilita y durante 100 ciclos se | |
| #desplazan los registros | |
| R1, R2, R3 = funcion_mayoria(R1, R2, R3, v_init) | |
| #Paso 5: Utilizando la funcion mayoria y habilitando la salida, se | |
| #desplazan los bits de cada registro durante 228 ciclos. Los bits mas | |
| #significativos de cada rehistro se operan con XOR y se crea un bit de | |
| #cifrado en cada iteracion | |
| R1, R2, R3, cl = clave_cifrado(R1, R2, R3) | |
| #Cifrado del mensaje | |
| mensaje_cifrado = cifrar(mensaje_original, cl) | |
| if DEBUG: | |
| print "*******************************" | |
| print "La clave de usuario es: " | |
| print clave | |
| print "*******************************" | |
| print "El vector de inicializacion es: " | |
| print v_init | |
| print "*******************************" | |
| print "El mensaje original es:" | |
| m = ''.join(str(e) for e in mensaje_original) | |
| print m | |
| print "*******************************" | |
| print "El mensaje cifrado es:" | |
| m2 = ''.join(str(e) for e in mensaje_cifrado) | |
| print m2 | |
| main() |
Results
Referencias
A5 Stream Cipher
A5/1
OK, 7.
ResponderEliminar