Obtenga la función de transferencia del sistema.
Para resolver esto tenemos la siguiente teoría obtenida del libro "Sistemas de Control Moderno" de Richard C. Dorf:
"y" es la única entrada y "u" la única salida y sus transformadas de Laplace son:
Como
tenemos:
Y ahora sustituimos X(s) en la ecuacion Y(s) y tenemos:
Entonces la funcion de transferencia:
es:

Entonces lo primero que hice es obtener la matriz Identidad multiplicada por s:
Después le resto la A:
Ahora obtenemos Phi(s):
Para obtener la matriz inversa se sigue la formula:
Entonces:
que es igual a:
y simplificamos la parte de abajo de la fracción:
Entonces ahora tenemos Phi(s)
El siguiente paso es obtener :
Sustituimos:
Entonces nuestra X(s) queda:
Ahora nuestra C es igual a la y que nos da el problema por las formulas ya vistas antes entonces tenemos que la C es:
Sustituimos valores:
Como podemos ver fácilmente la multiplicación de matrices será "s" , entonces tenemos:
La función de transferencia final es:
Y ahora si ya para terminar y por no quedarme con la duda me puse a investigar como podría hacer esto en octave, y encontré una función que se llama "ss2tf" en octave que lo que hace es que a partir de la variable de estados obtenemos la función de transferencia. Para esto lo primero que hay que hacer es instalar el paquete "signal" lo descargamos de la página oficial de octave, sin embargo al querer instalar este nos damos cuenta que tiene dependencias a otros paquetes que aun no están instalados:
Entonces igual descargo uno a uno los paquetes y instale primero el paquete "image" sin problemas, después el "specfun" también sin problemas y por último el "optim" con este si tuve que instalar otra vez otras dependencias:
También las descargo de la página de octave, y ahora si instalo "optim" y el paquete "signal" porfin.
Ahora en octave cargamos el paquete con "pkg load signal" y les dejo una captura con la solución de mi problema, primero cargamos las matrices de estado:
Y ahora resuelve y obtenemos el mismo resultado que encontramos a mano:
Referencias
Dorf, Richard C., and Robert H. Bishop. Sistemas de control moderno. 10th ed.
Matriz inversa
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
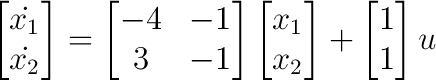
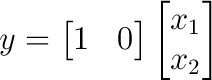
.gif)
.gif)
.gif)

.gif)
.gif)
.gif)

.gif)
.gif)
.gif)

.gif)
.gif)
.gif)



Muy bien; 15 pts.
ResponderEliminarGracias, por el aporte...
ResponderEliminar