Cálculo del pi en paralelo

En esta semana quise complementar lo de algoritmos paralelos haciendo un algoritmo que calcula el número Pi primero en paralelo y después en secuencial.

Metodo de Montecarlo

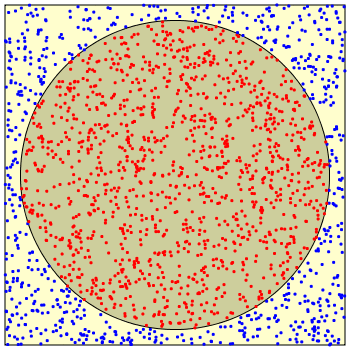
Este algoritmo consiste en generar experimentos aleatorios independientes consistentes en generar N puntos x, y que pertenezcan de 0 a 1 y contabilizar C los números que caen dentro del cuadrante de un circulo de radio 1.

El área del circulo es igual a pi*radio **2, el área del cuadrante es pi/4, y la probabilidad es C/N = pi/4 osea pi = 4C/N.

La aproximación más precisa es cuando N tiende al infinito.
Este es el algoritmo secuencial que desarrolle:


Ejecución:

Paralelización

Este reparto consiste en la generacion de N experimentos en un conjunto de P procesadores. Cada procesador puede generar puntos y contar cuales C caen en el rango del círculo con 1 de radio.
Al iniciar solo el proceso principal conoce cuales son los valores de N, osea el número de pruebas que se quiere hacer, y cuantos procesadores se van a tener.
Después se envian a los procesos esclavos la N, para que empiezen a calcular.

Cada proceso realiza el trabajo que le corresponde

Y por último los procesos esclavos envían sus resultados al proceso maestro, para que el maestro calcule el numero de aciertos y lo multiplique por 4 (por la formula que acabamos de ver) y lo divida entre el total de experimentos N.

Mi programa en python emula este comportamiento con hilos, y queue de python para poder mandar cada suma al proceso maestro, este es el programa:

En donde señale que sean 5 procesadores, osea 5 hilos que realicen la tarea indicada.

Y la ejecución se ve así:

El algoritmo lo desarrolle tomando la lo propuesto en este pdf, donde proponen la realización de él más no códigos ni pseudocódigos.