Online banking

Steganography

The images that I hide a message are the 001.png, 003.png and 005.png. I used big images because it can make more difficult to spot the changes.


I created two codes, one to hide the message and another to show the message:

Hide message

I used the LSB algorithm to encrypt the message. Before, I created a list with the phrase in binary. Then I put this bits in the LSB but I started to put the bits in the image  from the middle of the image and I used a space for each word of 10 bits.


Code:


Execution:

Recover the message

This is a little more complicated. I created an algorithm for look all LSB and then I search for differents sizes than can be the block of word. Once I find this, I start to check all the image and I get many data that can be the phrase that I want, but this doesn't make sense. Now I used a library that can help me to know if a word exist or not and automatically I get a phrase coherent.


Code:


Execution:

Library pyenchant python

Steganography

This is the group of images of which 3 have a hidden message:
Download

A5/1

A5 / 1 is used to provide privacy in outdoor communication with the GSM standard. An algorithm that encrypts the conversation between two GSM terminals when the message travels through the air.

History

A5/1 is used in Europe and the U.S. A5/1 is a very weak encryption algorithm, developed in 1987, when GSM was not even considered for use in Europe. A5 / 2 is a safer alternative that was developed in 1989.

Security

There are some well-known attacks to the algorithm A5 / 1. In some attacks, expensive preprocessing stages are required, after the code is attacked in minutes or seconds. The weakness of the algorithm had been passive attacks using the assumption of known plaintext. In 2003 were identified serious weaknesses that could be exploited ciphertext attacks (active attack). Eli Biham and Nathan Keller demonstrated attacks against A5 / 1 and A5 / 3 that allow the attacker to decipher the conversation in real time from a GSM phone.

Attacks with knowledge of the plaintext

In 1997, Golic presented an attack based on solving sets of linear equations of computational complexity 2 ^ 4016.
Also in 2000, Eli Biham and Orr Dunkelman published an attack with a complexity of 2 ^ 3991. This attack requires 32 GB of data stored after a previous stage of computing 2 ^ 38.


Description

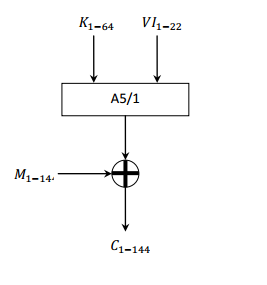
The transmission in GSM is performed in data blocks. Each block contains 114 bits available for information. A5 / 1 produces a 228-bit sequence of stream, which will serve as key encryption for message clear by Vernam algorithm (114 bits for a sense of call, and 114 for the other). It requires a user key of 64 bits (which is stored in the phone's SIM) together with an initialization vector 22 bits publicly known.

http://es.scribd.com/doc/25241410/46/Esquema-del-algoritmo-de-cifra-A5-1

The sequence of 86 bits (64 and 22 key vector) enters three shift registers LFSR linear feedback, for generating the encryption key by scrolling irregular following a majority function F. The output generated by the XOR

 http://en.wikipedia.org/wiki/A5/1

http://calliope.uwaterloo.ca/~ggong/ECE710T4/lec8-ch6b.pdf

Initializing A5

1. The three shift registers are set to zeros. The output and function are most disabled.
2. The least significant bit of each row applies XOR each bit of the key for 64 cycles. At this point, the LFSR normally works.
3. The least significant bit of each row applies XOR each bit vector Initialization for 22 cycles. The LFSR is working normally.
4. The majority function F is enabled for 100 cycles and moving logs, the Movement is made taking the result of F.
5. Using the majority function, and enabling the output of each shift register bitsduring 228 cycles. The most significant bits of each register are operated by XOR output, the result of this operation results in a bit of the encryption key.

Majority function

• F (C1, C2, C3) = C1 C2 ⊕ C1 C3 ⊕ C2 C3 where C1, C2, C3 are the clock bits for records R1, R2, R3, respectively.
• If the bit clock of a record matches the function majority, that record moves. Otherwise, the register keeps its value.
• This function majority forces at least 2 of the moving records at any time.
• Clock sequence is irregular and depends on the key and Frame Number.

Message Encryption

The clear message is operated by XOR with the first sequence of 144 bits (load data).

Code



Results

Referencias

A5 Stream Cipher
A5/1

IDEA

The IDEA(International Data Encryption Algorithm) was invented by Lai and Massey of Swiss Federal Institute of Technology in 1990. This algorithm is free for distribution in internet and is very popular in United States.

The International Data Encryption Algorithm was invented in Switzerland by the Chinese doctoral Lai and James Massey Xuejia when both worked in the Institute for Signal and Information Processing Federal Institute Swiss Technology in Zurich. It was patented in November 1991.

IDEA has been designed for the purpose of resisting certain attacks on in contrast with DES, which is vulnerable especially to the called "cryptanalysis differentials ". IDEA provides a key size safe enough.

The IDEA is a block cipher that operates on 64-bit sequences each cycle, ie, from 64 bits of plain text, obtained other 64 bits of ciphertext, as determined by a key of 128 bits size, which is more than enough with the current computational power to ensure invulnerability against exhaustive attacks.

The encryption algorithm is based on design concepts which blend operations from different algebraic groups. This property produces the best results against cryptanalysis.

Being a secret key algorithm, the procedure and the key Decryption is the same as that used for encryption. However, the IDEA algorithm is perfectly combinable with other asymmetrical algorithms.

A schematic description of the IDEA is presented next:

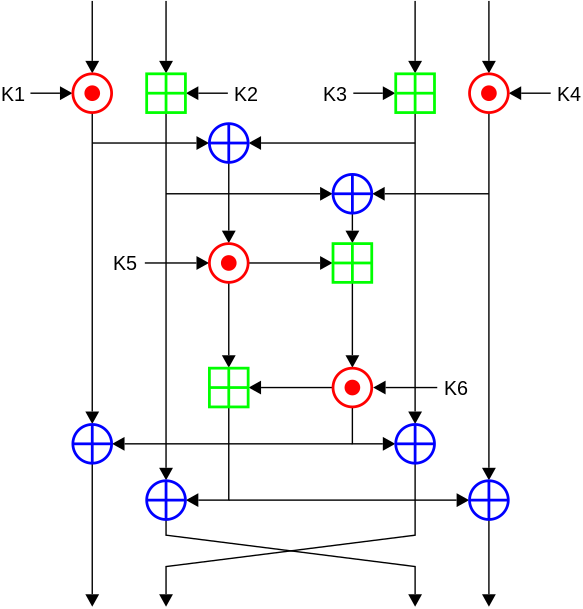[1]

In each elementary step by passing the text of 64 bits, this suffers from the following alterations to give the encryption:

1. Division of the 64-bit block of text into four sub-blocks of 16 bits: X1, X2, X3 and X4, and 128 of the key 8: Z1 ... Z8. These latter are intentionally more complicated and will be treated separately.
2. Multiplication of X1 for the first subblock of the key Z1
3. To this is added the second subblock X2 and Z2 key
4. To this is added the second subblock X3 and Z3 key
5. That is multiplied by X4 and for four key subblock
6. It is surgically exclusive OR (XOR) between the block result operations of the second and fourth operations
7. XOR between the result of the third and the fifth operation
8. Multiply the results of the sixth to the fifth operation key subblock, Z5
9. It adds the result of the sixth and seventh operations
10. Multiply the result from the ninth to the sixth operation key subblock, Z6
11. Add together the results of the eighth and tenth operation
12. XOR result of the second and the tenth
13. XOR the result of the fourth and tenth
14. XOR result of the third and eleventh
15. XOR the result of the fifth and eleventh

Thus is obtained the ciphertext, joining the four blocks from operations to the last four operations.

Clearly, the security of the cipher text increases when passing several times by the algorithm and perform IDEA 8 times. For feedback, simply swap the second and third blocks of exit and reenter them, in all stages except the last.

After the eighth round, there is a final transformation, which is described in the following four steps:

1. X1 Multiply by the first subblock of the key
2. Add X2 to the second key block
3. Add X3 the third key subblock
4. Multiplying X4 for the fourth subblock key

Finally, concatenate the last four blocks to get the output ciphertext.

The creation of the sub-blocks of the key, in the 1st step of the algorithm, consists in dividing the 128 bits of said key in the eight subblocks which only six are used in the first round, reserving two for second. After this, the key is rotated to the left 25 bits (Using the scroll function of the bits in the word provides the operator "<<"), and again the key is divided into eight subkeys. The first four subkeys are used in the second stage of the algorithm, and the last four in the third. The other key is rotated 25 bits to the left to get the eight following subkeys, and so on.

We use:

• Bitwise exclusive OR (denoted with a circled plus ⊕).
• Addition modulo 216 (denoted with a boxed plus ⊞).
• Multiplication modulo 216+1, where the all-zero word (0x0000) is interpreted as 216 (denoted by a circled dot ⊙).

Example

Message 1001 1100 1010 1100
Key 1101 1100 0110 1111 0011 1111

Encryption

Decryption

Efficiency and safety of IDEA

• IDEA is faster than DES even in software implementations.
• The 128-bit key is more resistant to attacks by "brute force".
• It is argued that IDEA is immune to the "differential cryptanalysis".
• There is evidence of weakness when using only two rounds instead of eight.
• We have discovered some sort of weak keys which could facilitate one chosen plaintext attack. For example, key type
  0000 0000 0x00; 0000 0000 000x; xxxx; x000
• IDEA supports operation modes ECB, CBC, CFB and OFB

References:

IDEA
[1] Imagen

RSA-based digital signatures

Homework:

"Implement a HTTP public-key repository for
key exchange that employs RSA-based digital
signatures."

I used Google App Engine Python for the web service, this is my app http://rsa-ds.appspot.com/.
The script to download and calculate the "r" and "y" is :



Google app python:



Database:

Screenshots:

Script:

App:

Result:

Script:

App:

Result:

App:

Result:

App:

Result:

RSA

For this week, the homework is to implement the RSA, I followed the next steps:

(the names of my variables are different than those we saw in class because I based the variable names on the book "Discrete Mathematics, Richard Johonsonbaugh"
)

• Create 3 scripts, one that generate public and private keys, another that is client.py and one for the server.py.

• For keys first generate a list of primes where I chose the p and q
• After, the n in my program is part of the public key. I chose the prime number as n. I noticed that phi is not a multiple of n.
• Immediately implements the Euclidean algorithm to get the s(private key)
• and finally create two key files, one public.txt and one private.txt
• I create the client.py and server.py and follow the next steps:

RSA:



Server:



Client:


Corrects users and keys:

Incorrect user:

Extra points

Extra points 1

The last week I choosed explain the following expressions:

c = m^e mod n

and

m = c^d mod n

For this example I used  m = 123(message), n = 3233, d = 2753.

c = 123¹⁷mod 3233 = 855
m = 855²⁷⁵³mod 3233 = 123

The property that make RSA invertible is:

m^ed-1≡1 mod n

To get the message after encription we have de following relations(_ku -public key, _kr-private key)

D_kr(E_ku(m)) = (m^e mod n)^d mod n ⇔ m ≡ m^ed mod n
                                                          ⇔ 1 ≡ m^ed-1 mod n

123¹⁷ mod 3233 = 855 ⇔ 123 =123^17*2753 mod 3233 ⇔ 1 = 123^17*2753-1 mod 3233

We need to be sure that  the values of e, d, n satisfy:

∀ m ∈ Z : m^ed-1 ≡ 1 mod n

Now is possible note that the first two expressions work in noth directions.
When we have decryption first and then encryption, the expression is equal to:

E_ku(D_kr(c)) = c ^de mod n ≡ c mod n

855^2753*17 mod 3233 ≡ 855 mod 3233 = 855

This is the correctness in the two directions.


References

Applied Cryptography

Diffie-Hellman

Excercise:

Hack manually (pencil and paper) a veryshort keyed Diffie-Hellman of your choice.

I have to find the x, y and k with the following numbers:

• X = 16
• Y = 13
• p = 17
• g = 5

And I have the formulas:

So, I did the following steps to find "x" and "k" using a "brute force attack":

And "y":

As we see  the both k(keys) are "1", with x=4 and y=8.

References

Algoritmos de intercambio de claves, Elisa Schaeffer

Statistical test

The homework is now testing my random key that I created the last week.

I have selected some random testing that I have used in this post.

First I generated 10 keys and created a file with all the keys, this file will be the input for the tests. This capture don't show all the file because this is very long.

I apply the monobit test and my 4 files passed, and this means that the secuency in that the 0 and 1 repeat are not predictable:

And then I applied the run test but, this didn't pass the test:

The next test is I made a compress my file, and this is the result:

So, we don't have security keys, because the file is compressed 16%.


In conclusion we can say that my keys are not secure because only passed 1 test of 3.

One-time pad

For this hw I have created a program that first reads a message from a file called "Message" then convert it to numbers, and then to binary.
Then I create a random key with the length of the binary string (that is saved in a file), and I apply XOR.
The result is encrypted message, now I created decrypt functions, and you can read the original message.
The code is all commented to understand him better.
I leave screenshot of several runs to see how it changes the encrypted message can fit the key.

Code:


Results: