Por ejemplo teniendo 1000 lectores diarios de la página de Internet, solo el 1% de ellos le dará click a algún anuncio, y así es como la página obtiene ganancias. Lo que a mi me interesa saber es la probabilidad de que el usuario numero Y sea el primero en dar click a algún anuncio.
Para elegir que modelo de distribución presenta este fenómeno primero analizare distintas distribuciones continuas y discretas.

Distribuciones discretas y continuas
Las distribuciones discretas son en las que la solución tiene un número determinado de valores.
Ejemplos:
El lanzamiento de una moneda al aire puede salir sol o cara, o si se lanza un dado podemos obtener un número del 1 al 6, si nace un bebe puede ser niño o niña, etc.
Las distribuciones discretas típicas son:
- El ensayo de Bernoulli
- La binomial
- La binomial negativa
- La geométrica
- La hipergeométrica
Las distribuciones continuas en las que las soluciones pueden tomar valores infinitos de cierto intervalo.
Ejemplo: El peso de cada integrante de alguna familia (43.3, 55.2, 87,1), o la edad de las personas que toman algún camión (12.3, 45.5, 32.1, 76.4).
Las distribuciones continuas típicas son:
- Poisson
- Exponencial
- Distribución de Gauss o normal
Volviendo al modelo que elegí creo que es una distribución discreta ya estoy buscando simplemente el éxito o el fracaso, es decir si da click o no da click, algo muy parecido al ejemplo de las monedas, o de los dador, usaré para explicar mi modelo la distribución geométrica.
Distribución geométrica
En la distribución geométrica se supone que se lleva a cabo una secuencia de ensayos de Bernoulli independientes, en dónde cada uno tiene la misma probabilidad de éxito "p". "X" es el número de experimentos hasta que se incluye el primer éxito. Entonces X es una variable aleatoria discreta en dónde tenemos una distribución geométrica con parámetro "p".
La podemos expresar X ~ Geom(p).
Ahora mi problema es el siguiente:
En una página web tiene ingresos a través de anuncios publicitarios en la esquina de la página, cada que un usuario da click son ganancias para la página, Si solo el 1% de los usuarios que entran a la página dan click a anuncios, ¿cuál será la probabilidad de que al usuario 2 de el primer click en algún anuncio?
Esto lo podemos representar de esta manera:
P(X = 2) = P(fracaso)(éxito) = P(0.9)(0.1) = 0.09
y de que la 10ma persona de click por primera vez es:
P(X = 10) = P(fr)(fr)(fr)(fr)(fr)(fr)(fr)(fr)(fr)(éxito)
P(0.9)^9 (0.1) = 3.874204889999999e-12
La función que describe esta distribución es:

Ahora para cambiar un poco podemos plantearlo de manera un poco diferente, para tener una probabilidad de 100% de que la persona dará click ¿Cuántos experimentos necesitamos hacer?
La manera de resolverlo es despejando la x de le ecuación, con la fórmula anterior:

Versión continúa de distribución geométrica
La versión continua de esta distribución es: La distribución exponencial. Se utiliza para modelar el tiempo entre eventos sucesivos, o el tiempo requerido para dar servicio a un evento. La distribución exponencial tiene la propiedad de no tiener memoria, es decir, conociendo el tiempo que el último evento ocurrió no se puede predecir cuando el evento siguiente puede ocurrir.
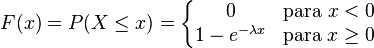
¿Mi modelo puede ser continuo?
Aplicación a mi problema, exactamente con la redacción que tiene no es un fenómeno continuo, pero si se empieza a checar en términos de tiempo, es decir cuantas veces se dio click al anuncio en una hora, o en un minuto, ahí si se convierte en fenómeno continuo.
Código, el código que tomé para hacerlo continuo es el hecho en clase, en dónde tenemos declaradas las variables p (parámetro que significa portabilidad), q que es 1 - p y k que corresponde al intervalo.
De manera discreta observamos algo así para el caso en dónde la probabilidad es .1 y .2, .5 y .9
en las grágicas el color rojo representa la probabilidad 0.1, verde .2, azul .5 y celeste .9.

Ahora para hacerla continua lo primero que se me ocurrió fué reducir el intervalo que es en la variable k, entonces lo hice aumentando .1 en .1 en vez de 1 en 1, y lo que obtuve fué lo siguiente:

Vemos que no se ve muy bien, entonces me di cuenta que para mantener la curva como en la discreta la probabilidad osea p también disminuye, osea si dividí en 10 el avance de k la p también tenia que hacerlo, ya que no es posible que para ahora 1000 intervalos en vez de 100 cada intervalo que se hizo mas pequeño tenga la misma probabilidad que lo que eran 10 veces más grandes, entonces ahora p la dividí entre 10 y obtuve esto:

Aquí están las modificaciones:
Espero comenten y me den algunas ideas para el programa.
Fuentes
Libro: Estadística para Ingenieros y científicos de William Navidi, Capitulo 4.
grágicas
ResponderEliminarMuy bien el reporte y también el programa me agrada. Ahora le puedes aplica lo de distancia total de variación para ver si en realidad es la distribución exponencial :)
Van 5+5.